Alright so - I think I want to walk through a couple things today re: Post Fiat’s consensus model. In XRP world, a Swiss foundation selects the Unique Node List (which validates on chain transactions). And this XRPL foundation is pretty opaque. In Post Fiat, the methodology is transparent. And it’s powered by LLMs and in this blog post I want to talk about exactly how that works
The TLDR is that it’s possible to use LLMs to deterministically make judgments about things. And you don’t need open source models to do it.
Before we get into validator scoring - let’s just go through a super basic example
You can use the code in this Gist File to reproduce my results for the images below
Exhibit 1: Establishing Basic LLM Responses

Exhibit 1 shows that. If you run an LLM 100 times with instructions to generate a number from 0-300 on different machines with the same model and settings it will output the same answer consistently with zero variation. You can reproduce all the examples above on your machine given the same settings as in the demo (see Sample Code)
So basically in this image you can see “A blue whale dives”. If you jam that through Claude Haiku 100 times with the instructions to return a number between 0 and 300 you always get 120. This sounds mundane but it’s what makes LLMs different from conscious communication. You basically get deterministic outputs.
That’s also why you can predict what LLMs are going to say. They are literally designed to be predictable via compression - i.e. they are predicting the next token. That’s what they are. More on this in a bit
So this is level 1 of understanding it. The photo above basically shows that if you run 30 different queries 100 different times you always get the same mode. But interestingly, outside of Mode, LLMs also have a finger print. So check out the table below
Exhibit 2: Standard Deviation Fingerprints
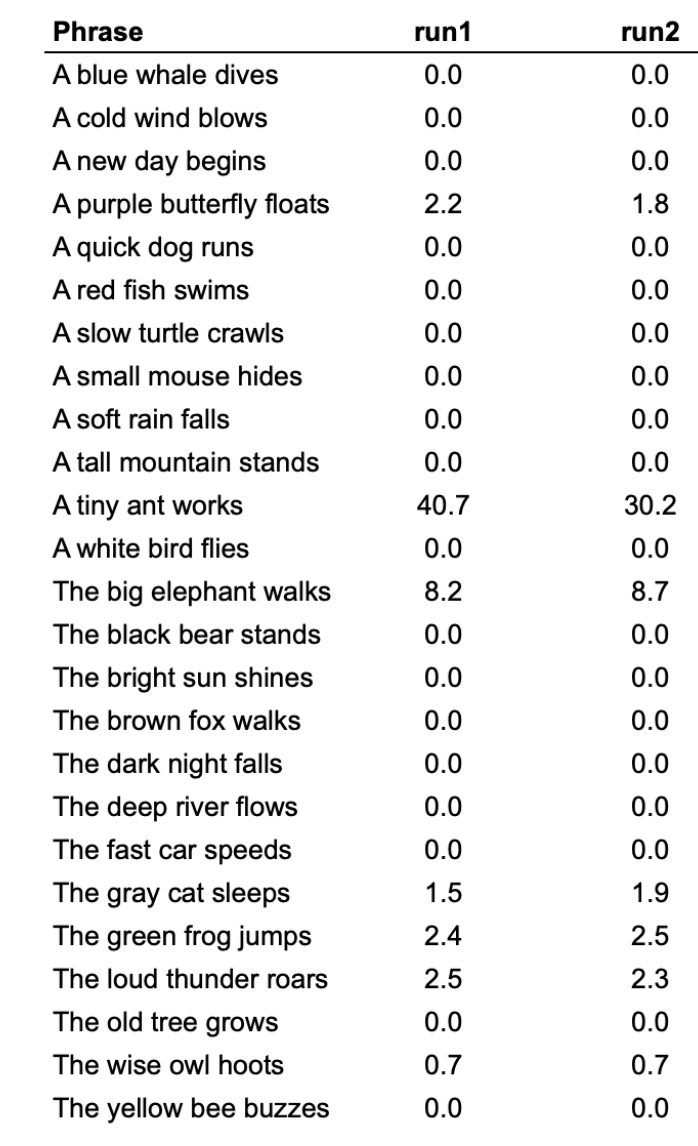
These are the standard deviations from running those terms through Claude Haiku. “A blue whale dives” has 0 standard deviation. But “A tiny ant works” has a very high standard deviation in relative space. That is to say, if you run it 100 times – it’s likely to generate more different results from Claude Haiku. This standard deviation property creates a finger print such that if you’ve run a model a bunch of times you know which one has run. Even if you don’t have the model weights.
If you gave someone this list of phrases and numbers you could know that someone was running Claude Haiku, without them telling you. You are probably seeing where this is going.
Exhibit 3: Validator Scoring
So now we’ve established the idea that you can deterministically score random strings and output numbers the question is can you output something that actually makes sense. For this example we use are the URLs of all the Doxed Validators on XRP Unique Node List.
You can find this list here: XRP Scan
So you can see we have a bunch of different validators ranging from the University of Waterloo to XRPGoat.com. And in this exercise we are going to score them.
So getting into the prompting - here’s what we’re using for the User Prompt
You are the Post Fiat validator judgment system. You are presented with a single validator URL and output 50 word responses.
Your job is to take the following URL and output a 50 word statement with three key attributes:
- The name of the organization that the URL represents
- A brief comment on how credible the organization is. Credibility should consider: A. The market cap or size of the organization – ie pure institutional size economic or societal weight (high scores should favor huge institutions) B. The censorship resistance of the organization – ie ability to withstand pressure from governments (high scores would favor independent - strong institutions) C. The technological capability to conform rapidly with network upgrades (high scores would favor highly technical adept institutions)
- An integer score from 0-100 indicating how credible the organization is. A score of 100 means the organization is highly credible, a score of 0 means the score is unknown or not credible at all
- A sovereign such as a government or Central Bank should have a score of 100
- A megacap corporation should have a score of at most 85 (with midcap corporations getting 75 max and microcaps getting 50 max)
- A globally renowned university should have a score of 100 with lesser schools getting lower scores
- A hobbyist website or unknown organization that is not in the training data should get a score of at most 35
- If the organization is Centralizing - i.e. likely tied to Ripple Labs then the score should be at most 55
URL to analyze: {url}
So basically we apply this to the Validators. You can find the example code here (note you need an OpenRouter API Key) output
So we can see the top performing validators here
shadow.haas.berkeley.edu Organization: UC Berkeley Haas School of Business\n\nCredibility Assessment: This is a prestigious public university business school with significant institutional weight and academic reputation. However, as an educational institution, it has moderate censorship resistance and limited technical infrastructure for rapid network upgrades compared to specialized technology organizations. Score: 85
ripple.ittc.ku.edu Organization: University of Kansas Information and Telecommunication Technology Center (ITTC)\n\nCredibility Assessment: ITTC is a legitimate research center at a major state university with strong technological capabilities and academic independence. However, it has moderate institutional size compared to global megacorps or sovereign entities, and limited censorship resistance as a state-funded institution. Score: 75
And the lowest performing validators here **ekiserrepe.es ** Organization: Ekiserrepe.es appears to be an unknown Spanish website or domain with no clear organizational identity or public presence.\n\nCredibility Assessment: This organization lacks institutional size, has no demonstrated censorship resistance capabilities, and shows no evidence of technological expertise for network operations. The domain appears to be either inactive, personal, or represents a very small entity with minimal public footprint. Score: 15
jon-nilsen.no - Organization: Jon Nilsen (Individual/Personal Website)\n\nCredibility Assessment: This appears to be a personal website belonging to an individual named Jon Nilsen. As a personal site with no apparent institutional backing, it lacks significant economic weight, censorship resistance, and proven technical capabilities for network operations.\n\nScore: 15\n\nThe low score reflects the individual nature of this validator, limited institutional size, uncertain technical capabilities, and lack of established credibility in blockchain validation katczynski.net- Organization: Katczynski.net appears to be a personal website or blog, likely referencing Theodore Kaczynski (the Unabomber). \n\nCredibility Assessment: This is a small personal website with minimal institutional size, unknown technological capabilities, and unclear governance structure. While potentially censorship-resistant due to its independent nature, it lacks the scale, resources, and established reputation necessary for high credibility in validator operations. Score: 15
And the thing is if you run this 100 times – you will converge upon the exact same scores, with the exact same description for each validator. And as you can see the scores actually make sense.
There are some hacks to make this work including
- setting temperature to zero
- Being very specific about prompt outputs – specifying the number of sentences or format for the output helps a lot
But these work across almost all major models. Open source, closed source, doesn’t matter. And what this means is that we can trustlessly verify the credibility of validators. Determining if they should be on the network or not. And also figure out how much they should earn for validating the network.
Conclusions
So this basically shows you how the Post Fiat consensus works. And it is robust to Closed vs Open Source debate which is different than any Crypto AI protocol. If anything we actually might opt into closed source models because the compliance benefits are more important for banks than the open source models, because – per the analysis above, it works just fine so long as you have access to the model. This obviously will be upsetting to a lot of people in crypto, but will be a big positive to banking validators. Which is part of our chain selection. To go full circle.
Anyways – this is a pretty cool overall property. The ability for us to agree on things assuming we have a model is a really underexplored areas with lots of applications to the law, DAOs, philosophy, investing and many other areas. But it is essential for the Post Fiat network to work. Will end with some supplemental formulas – if you’re a PHD interested in helping with the white paper please email me at [email protected]
The Mathematical Foundation
Temperature-Scaled Softmax
The probability of selecting token $x_t$ given context:
$$p(x_t | x_{<t}) = \frac{\exp(h_t^T w_{x_t} / \tau)}{\sum_{v \in V} \exp(h_t^T w_v / \tau)}$$
Where:
- $h_t$ = hidden state encoding all context
- $w_v$ = learned output embeddings
- $\tau$ = temperature parameter
- $V$ = vocabulary
Mode Collapse at Low Temperature
As $\tau \to 0$:
$$\lim_{\tau \to 0} p(x_t | x_{<t}) = \mathbb{1}[x_t = \arg\max_v h_t^T w_v]$$
This creates deterministic greedy decoding.
Information Bottleneck Objective
Models optimize:
$$\min_{T} I(X;T) - \beta I(T;Y)$$
Where:
- $I(X;T)$ = mutual information between input and representation (minimized)
- $I(T;Y)$ = mutual information between representation and output (maximized)
- $\beta$ = trade-off parameter
Consensus Probability
The probability of validator agreement:
$$P(\text{consensus} | x, \tau) \geq 1 - \epsilon$$
Where $\epsilon \to 0$ as:
- $\tau \to 0$ (temperature approaches zero)
- $I(X;T|Y) \to 0$ (task-irrelevant information compressed)
- Models converge to universal representations
Practical Implementation
For validator scoring with $n$ validators and $m$ models:
$$\text{Score}{final}(v_i) = \text{mode}{\text{Score}{M_j}(v_i)}_{j=1}^{m}$$
With verification: $$\text{Valid} = \mathbb{1}[\sigma(\text{Score}{M_j}(v_i)) = \sigma{expected}]$$
Where $\sigma$ represents the standard deviation fingerprint unique to each model.
Why Rank Convergence Dominates Value Convergence
Value vs Rank Probability
For two models $M_1$ and $M_2$ scoring validators $v_i$:
Value Agreement: $$P(\text{Score}{M_1}(v_i) = \text{Score}{M_2}(v_i)) = p_{value} < 1$$
Rank Agreement: $$P(\text{Rank}{M_1}(v_i) = \text{Rank}{M_2}(v_i)) = p_{rank} \gg p_{value}$$
Mathematical Inevitability
Given $n$ validators with scores $S = {s_1, s_2, …, s_n}$:
- Possible value configurations: $101^n$ (for scores 0-100)
- Possible rank configurations: $n!$
Since $n! \ll 101^n$ for any reasonable $n$, rank space is vastly smaller.
Preserved Ordering Under Monotonic Transformations
If models learn similar concepts but with different scaling:
$$\text{Score}{M_2}(v) = f(\text{Score}{M_1}(v)) + \epsilon$$
Where $f$ is any monotonic function and $\epsilon$ is small noise.
Then for any validators $v_i, v_j$: $$\text{Score}{M_1}(v_i) > \text{Score}{M_1}(v_j) \iff \text{Score}{M_2}(v_i) > \text{Score}{M_2}(v_j)$$
This preserves ranks even when values differ!
Empirical Correlation
The Spearman rank correlation approaches unity:
$$\rho_s = 1 - \frac{6\sum d_i^2}{n(n^2-1)} \approx 0.995$$
Where $d_i$ = difference in ranks for validator $i$.
This 0.995+ correlation emerges because:
- Models share universal semantic representations
- Rank ordering is invariant to linear transformations
- Information bottleneck preserves relative relationships
Bottom line: You don’t need exact value agreement. Rank agreement is mathematically inevitable when models share the same conceptual understanding.